Abstract
Transformers are very powerful for language tasks and training is ****faster on GPUs because of parallization, but they use a lot of memory and computing power, especially when processing long text, their cost grows very fast (quadratically).
RNNs, on the other hand, use less memory and computation cause they grow linearly but are slower to train and not as good at handling long sentences.
The new model RWKV mixes the good parts of both, it trains quickly and gets good performance like a Transformer and also runs efficiently like an RNN.
1 Introduction
RWKV reformulates the attention mechanism with a variant of linear attention, replacing traditional dot-product token interaction with more effective channel-directed attention. This implementation, without approximation, offers the lowest computational and memory complexity.
2 Background
2.1 Recurrent Neural Networks (RNNs)
Popular RNN architectures such as LSTM and GRU. Although these RNNs can be factored into two linear blocks (W and U) and an RNN-specific block, the data dependency relying on previous time steps prohibits parallelizing these typical RNNs.
| Model | Depends on | Parallelizable? |
|---|---|---|
| RNN | computed previous state | ❌ No |
| RWKV | raw previous input | ✅ Yes (for training) |
2.2 Transformers and AFT
Standard Transformer self-attention
Matrix form
Per token (t)
- The weighted value equation in multi-head attention.
- Weight of token $i$ for query $t$ is $\exp(q_t^\top k_i)$.
- Output is a weighted average of $v_i$
AFT (Attention-Free Transformer) variant
- Replace $q_t^\top k_i$ with (learned) position bias $w_{t,i}$ + a key score $k_i$.
- Causal: sum only $i\le t$.
- Still a normalized weighted average, but weights depend on position via $w_{t,i}$.
RWKV’s simplification
Define the bias as a decay with distance:
- Per-channel vector $w$ ⇒ older tokens get weight $e^{-(t-i)w}\le 1$.
- Now weights depend only on how far back a token is, not on $q_t$.
- This structure lets us keep running sums, so we don’t need all pairwise scores.
Result:
Same attention-like effect, but computed with O(T) time and O(1) memory per step (like an RNN), while still trainable in parallel across tokens (like a Transformer) by prefix-scan tricks.
| Model | Has Query? | How it computes weights | Complexity | Key idea |
|---|---|---|---|---|
| Transformer | ✅ Yes | all tokens attend to all | O(N²) | Full pairwise attention, strong but heavy |
| AFT | ❌ No | Uses position bias | O(N) | Removes query, uses learned positional weights |
| RWKV | ❌ No | Adds time-decay weights | O(N) | AFT idea + RNN-style update (linear, efficient) |
3 RWKV
Four fundamental elements:
- R: The Receptance vector acts as the receiver of past information.
- W: The Weight signifies the positional weight decay vector, a trainable parameter within the model.
- K: The Key vector performs a role analogous to K in traditional attention mechanisms.
- V: The Value vector functions similarly to V in conventional attention processes.
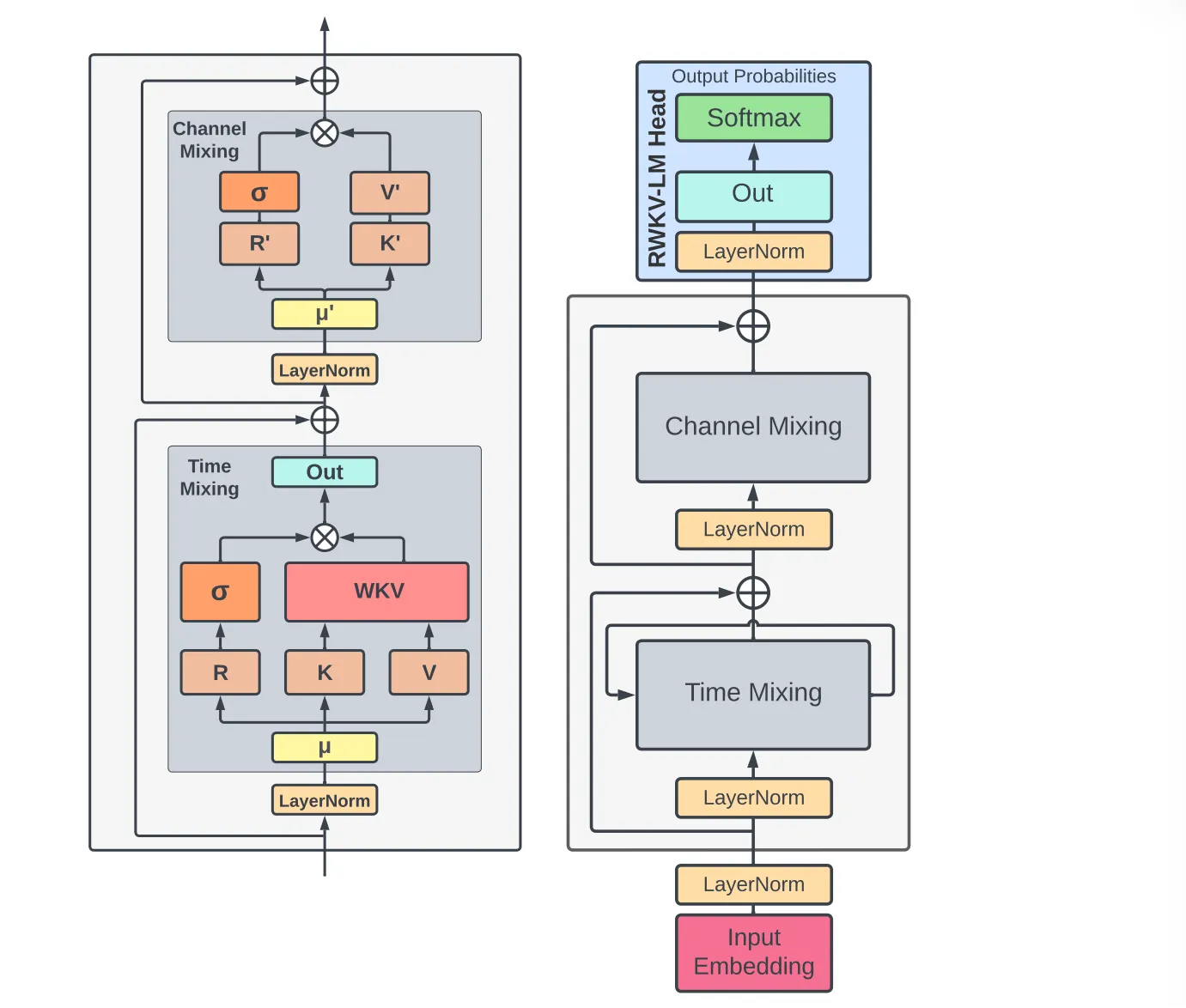
3.1 Architecture
The RWKV model is composed of stacked residual blocks. Each block consists of a time-mixing and a channel-mixing sub-block, embodying recurrent structures to leverage past information.
This model uses a unique attention-like score update process, which includes a time-dependent softmax operation improving numerical stability and mitigating vanishing gradients. It ensures that the gradient is propagated along the most relevant path. Additionally, layer normalization incorporated within the architecture aids in stabilizing the gradients, effectively addressing both vanishing and exploding gradient issues.
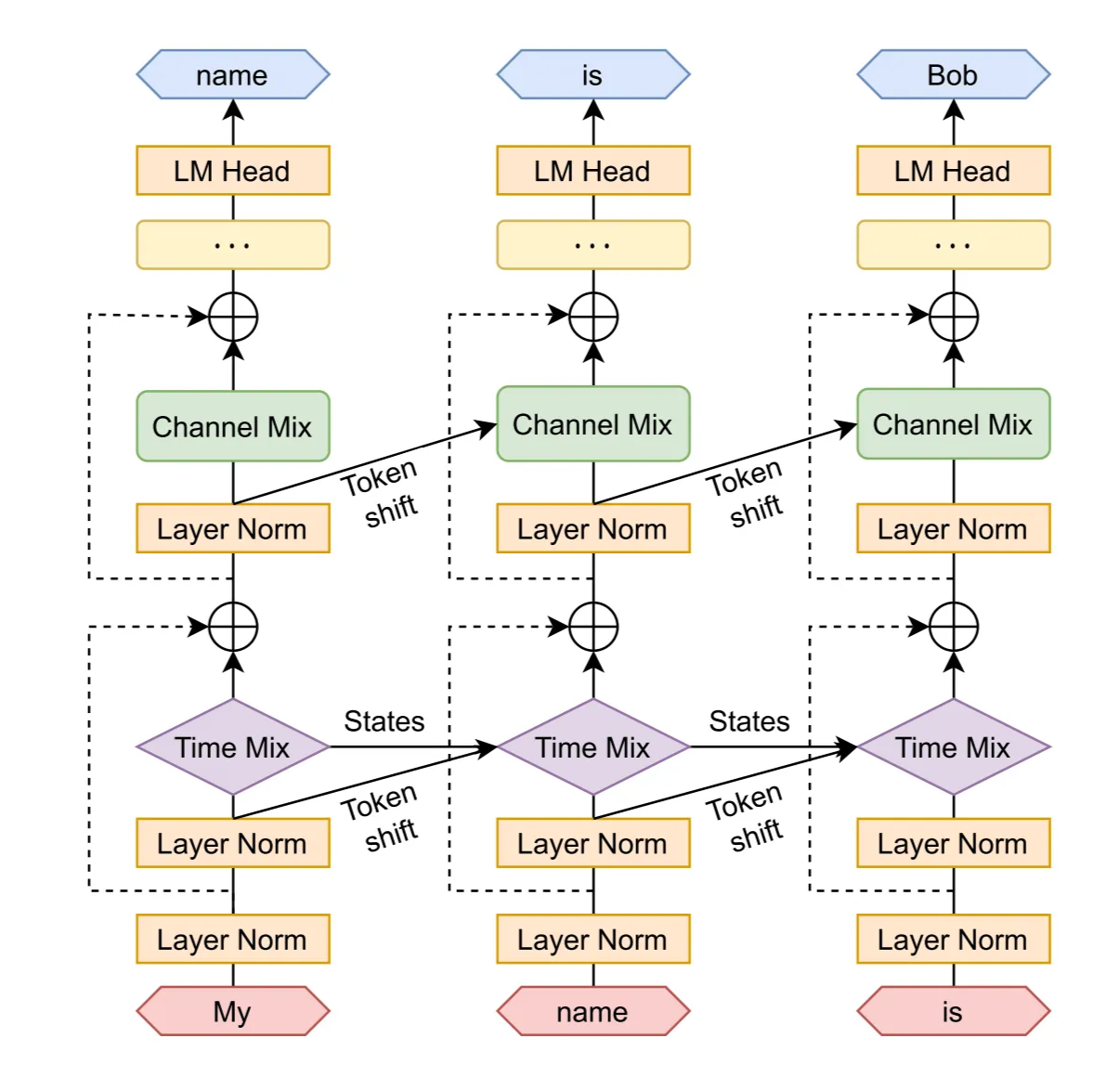
3.1.1 Token Shift
In this architecture, all linear projection vectors (R, K, V in time-mixing, and R′, K′ in channel- mixing) involved in computations are produced by linear interpolation between current and previous timestep inputs, facilitating a token shift.
The vectors for time-mixing computation are linear projections of linear combinations of the current and previous inputs of the block:
The channel-mixing inputs:
3.1.2 WKV Operator
3.1.3 Output Gating
Time Mixing:
Channel Mixing:
4 Trained Models and Computing Costs
Adam optimizer, bfloat16 precision, the auxiliary loss introduced by PaLM…
4.2 Scaling Laws
Scaling laws in language models refer to the mathematical relationships that describe how the performance of a language model changes with respect to various factors.
Scaling laws are important for two primary reasons:
- they allow us to make predictions and plans regarding the costs and performance of large models before they are trained via interpolation and extrapolation.
- the contexts in which they fail provides rich feedback on important areas for future research.
5 Evaluation
Evaluation direction and questions:
Competitiveness: Tests if RWKV performs as well as Transformers when both use the same computing power.
Long Context: Tests if RWKV can handle very long texts better than Transformers,
especially when Transformers become too slow or costly for long sequences.
6 Inference Experiments
float32 precision, the HuggingFace Transformers,
7 Future Work
1. Increase Model Expressivity
- Improve time-decay formulas.
- Explore better initialization of model states.
- Goal: more powerful representations without losing efficiency.
2. Improve Computational Efficiency
- Use parallel scan in $wkv_t$ step.
- Target complexity: $O(B \log(T)d)$.
3. Apply to Encoder–Decoder Architectures
- Replace cross-attention with RWKV mechanism.
- Useful for seq2seq and multimodal models.
- Boosts efficiency in both training and inference.
4. Use of Model State (Context)
- Used for interpretability and predictability.
- Could enhance safety and control via prompt tuning.
- Modify hidden states to guide model behavior.
5. Larger Internal States
- Improve long-term memory and context understanding.
- Increase performance across various tasks.
8 Conclusion
We introduced RWKV, a new approach to RNN models exploiting the potential of time-based mixing components. RWKV introduces several key strategies that allow it to capture locality and long-range dependencies while addressing limitations of current architectures by: (1) replacing the quadratic QK attention with a scalar formulation at linear cost, (2) reformulating recurrence and sequential inductive biases to enable efficient training parallelization and efficient inference, and (3) enhancing training dynamics using custom initializations.
We benchmark the proposed architecture in a wide variety of NLP tasks and show comparable performance to SoTA with reduced cost. Further experiments on expressivity, interpretability, and scaling showcase the model capabilities and draw parallels in behavior between RWKV and other LLMs.
RWKV opens a new route for scalable and efficient architectures to model complex relationships in sequential data. While many alternatives to Transformers have been proposed with similar claims, ours is the first to back up those claims with pretrained models with tens of billions of parameters.
9 Limitations
1. Performance Limitation (Memory Loss over Long Contexts)
- Linear attention is efficient but may lose fine details over long sequences.
- RWKV compresses history into a single vector, unlike Transformers that keep all token interactions.
- Its recurrent design limits ability to fully “look back” at distant tokens.
2. Dependence on Prompt Engineering
- RWKV relies more on well-designed prompts than Transformers.
- Poor prompts may cause information loss between prompt and continuation.