Abstract
The paper revisits LSTMs, whose key innovations are the constant error carousel and gating mechanisms — originally solved the vanishing-gradient problem and made long-term memory possible. Although Transformers later surpassed LSTMs thanks to their parallelizable self-attention, the authors ask whether LSTMs can be scaled up, like modern LLMs, to billions of parameters while overcoming their known limits.
To achieve this, they introduce:
- Exponential gating — a new gating function with improved normalization and stability.
- Modified memory structures:
- sLSTM — uses scalar memory and scalar updates with new “memory mixing.” → memory mixing
- mLSTM — introduces matrix-based memory that supports full parallelization and a covariance-based update rule. A new memory architecture → parallelization
By stacking these enhanced cells into residual xLSTM blocks, they create architectures that combine the strengths of LSTMs and Transformers.
Experiments show that xLSTMs can match or even outperform Transformers and State Space Models in both performance and scaling.
👉 Code: github.com/NX-AI/xlstm
1 Introduction
1.1 LSTM

$$ c_t = f_t c_{t-1} + i_t z_t, \quad h_t = o_t \psi(c_t) $$
- Update the cell state / long-term memory:
$$ c_t = f_t c_{t-1} + i_t z_t $$
- $c_t$: Cell state, real-valued vector, the internal long-term memory after update
- $f_t$: Forget gate, values in (0, 1), decide how much of $c_{t-1}$ to keep
- $c_{t-1}$: Previous cell state, vector, carries long-term memory
- $i_t$: Input gate, values in (0, 1), decides how much new info to write
- $z_t$: Cell input / candidate memory, usually $\tanh(\cdot)$ output, the new content that could be added
- Produce the output / hidden state / short-term memory:
$$ \quad h_t = o_t \psi(c_t) $$
- $h_t$: Hidden state, vector, output of the cell (short-term memory)
- $o_t$: Output gate, values in (0, 1), controls what part of memory is shown outside
- $\psi(c_t)$: Activation function (often $\tanh(c_t$)), squashes memory to bounded range
Three Main Limitations of LSTMs
- Can’t revise stored information
- Once an LSTM stores something in its cell state, it struggles to update or replace it later.
- xLSTM fix: introduces exponential gating, allowing flexible updating of stored values.
- Limited storage capacity
- Traditional LSTMs store information in a single scalar cell state, forcing compression and loss of details.
- xLSTM fix: uses a matrix memory, which can hold richer, multi-dimensional information.
- No parallelization
- LSTM depends on sequential hidden-to-hidden connections, meaning each step waits for the previous one.
- xLSTM fix: changes the memory mixing structure to make computation parallelizable across time steps.
2 Extended LSTM
- Two main modifications: exponential gating and novel memory structures.
- Two variants mombined into xLSTM blocks, stacked with residual connections to build xLSTM architectures, both can have multiple memory cells and heads:
- sLSTM – scalar memory, scalar update, memory mixing across cells.
- mLSTM – matrix memory, covariance (outer product) update, fully parallelizable.
2.2 sLSTM
sLSTM = LSTM + exponential gates + normalization state + stabilizer state + multiple memory cells.
The exponential gates $i_t$ and $f_t$ make it easier to amplify or reduce memory dynamically.
→ Helps sLSTM revise stored information better (a key limitation of classical LSTM).
The normalizer state $n_t$ keeps things numerically stable, so exponential growth doesn’t blow up.
The stabilizer state $m_t$ keeps their scale controlled, prevents numerical overflow during training.
The Multiple heads each with its own LSTM-like structure to compute its own $h_t$, then combined, just like multi-head attention in Transformers, allowing the network to learn different kinds of temporal patterns in parallel.

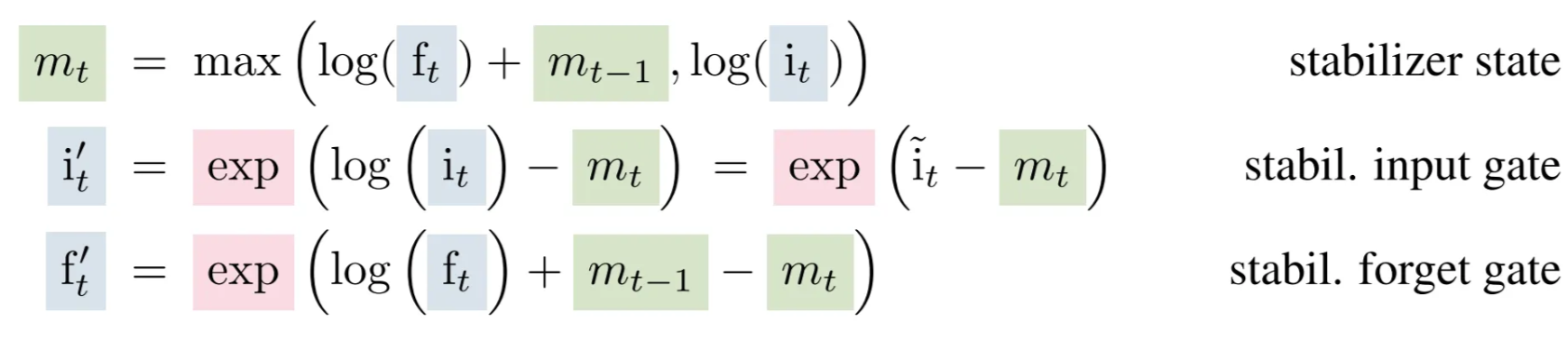
2.3 mLSTM
mLSTM = LSTM + exponential gates + normalization state + stabilizer state + multiple memory cells.
mLSTM replaces the small one-number memory $c_t$ of LSTM with a key–value memory matrix, so it can store, search, and update information like attention, but still works as a recurrent network (RNN).
- $q_k, k_t, v_t$ → same like query, key, value in transformer…
- uses a matrix memory because it wants to store relationships between features (keys and values), not just single values like traditional LSTM.
- The normalizer state $n_t$ is the weighted sum of key vectors, keeps record of the strength of the gates.
- Multiple heads and multiple cells are equivalent as there is no memory mixing.
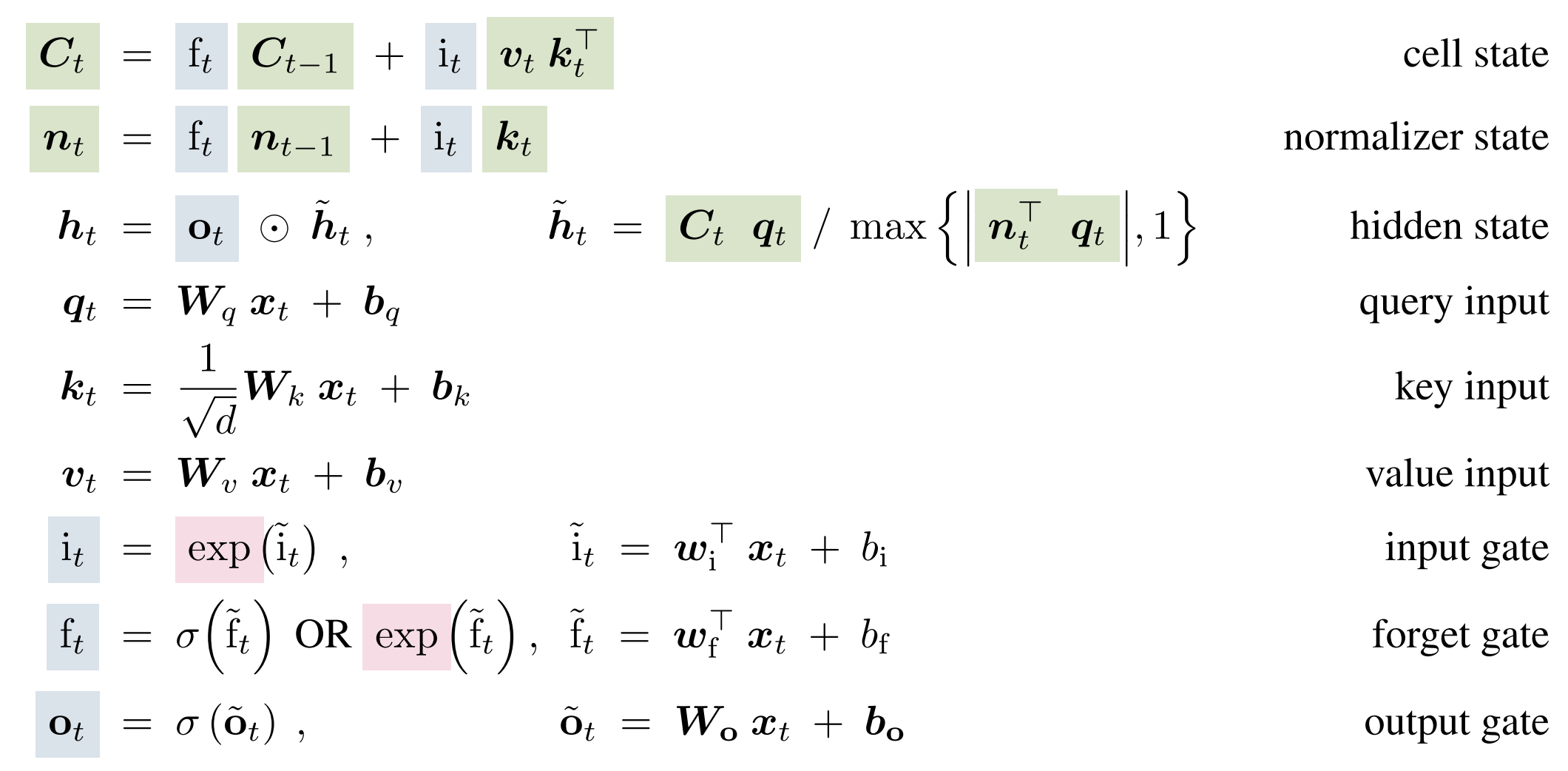
2.4 xLSTM Architecture
2.4.1 xLSTM Blocks
Each block takes an input (sequence or features), passes it through an sLSTM or mLSTM cell, adds some non-linear layers (MLPs) and residual/skip connections, finally outputs a transformed sequence representation.
| Type | Memory type | Recurrent connections | Parallelization | Up-proj position | Storage capacity | |
|---|---|---|---|---|---|---|
| sLSTM | Post up-projection | Scalar memory (vector) | ✅ via matrices R | ❌ Sequential | after LSTM | Smaller |
| mLSTM | Pre up-projection | Matrix memory | ❌ No recurrent matrices | ✅ parallelizable | before LSTM | Much larger |
2.4.2 xLSTM Architecture
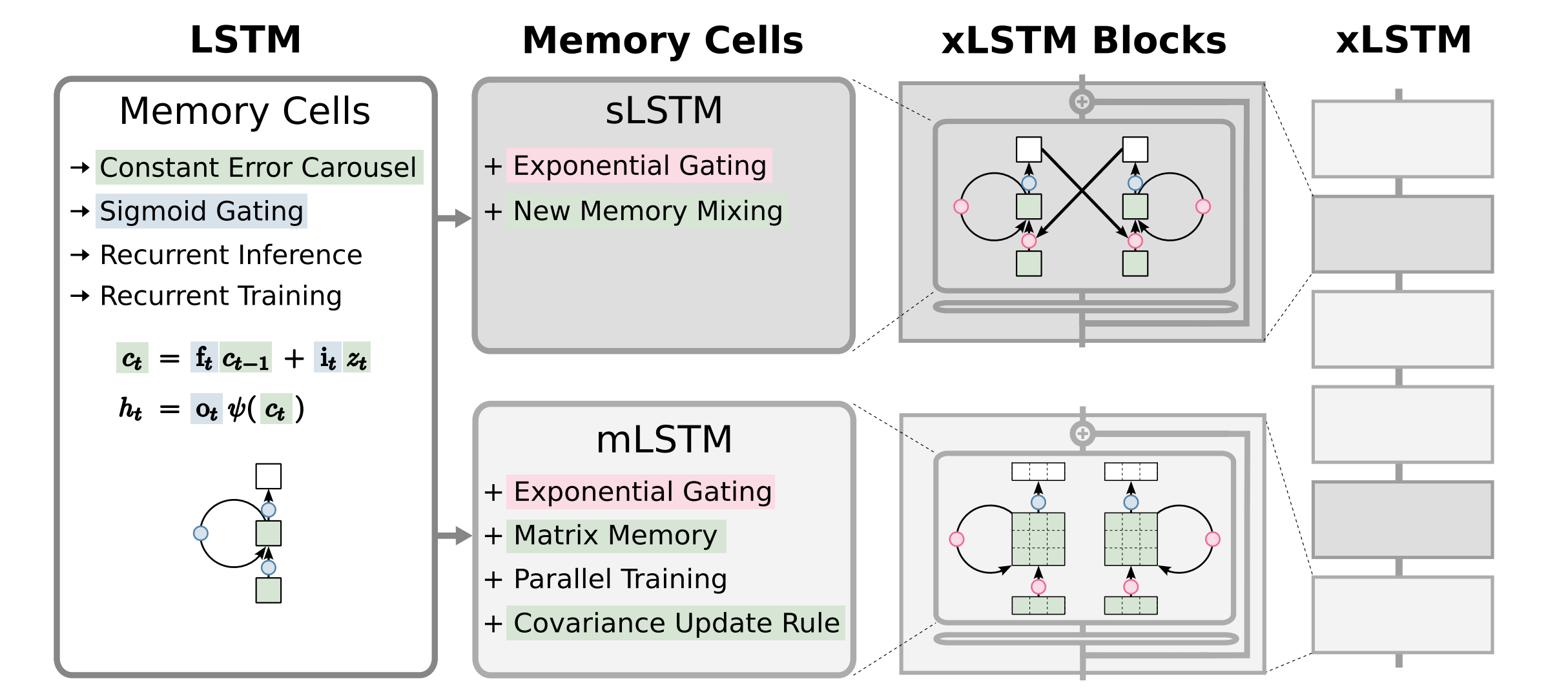
The constant error carousel is the additive update of the cell state $c_{t−1}$ (green) by cell inputs $z_t$ and moderated by sigmoid gates (blue).
The gating mechanisms:
- Forget gate decides what to erase.
- Input gate decides what to add.
- Output gate decides what to show.
4 Experiments
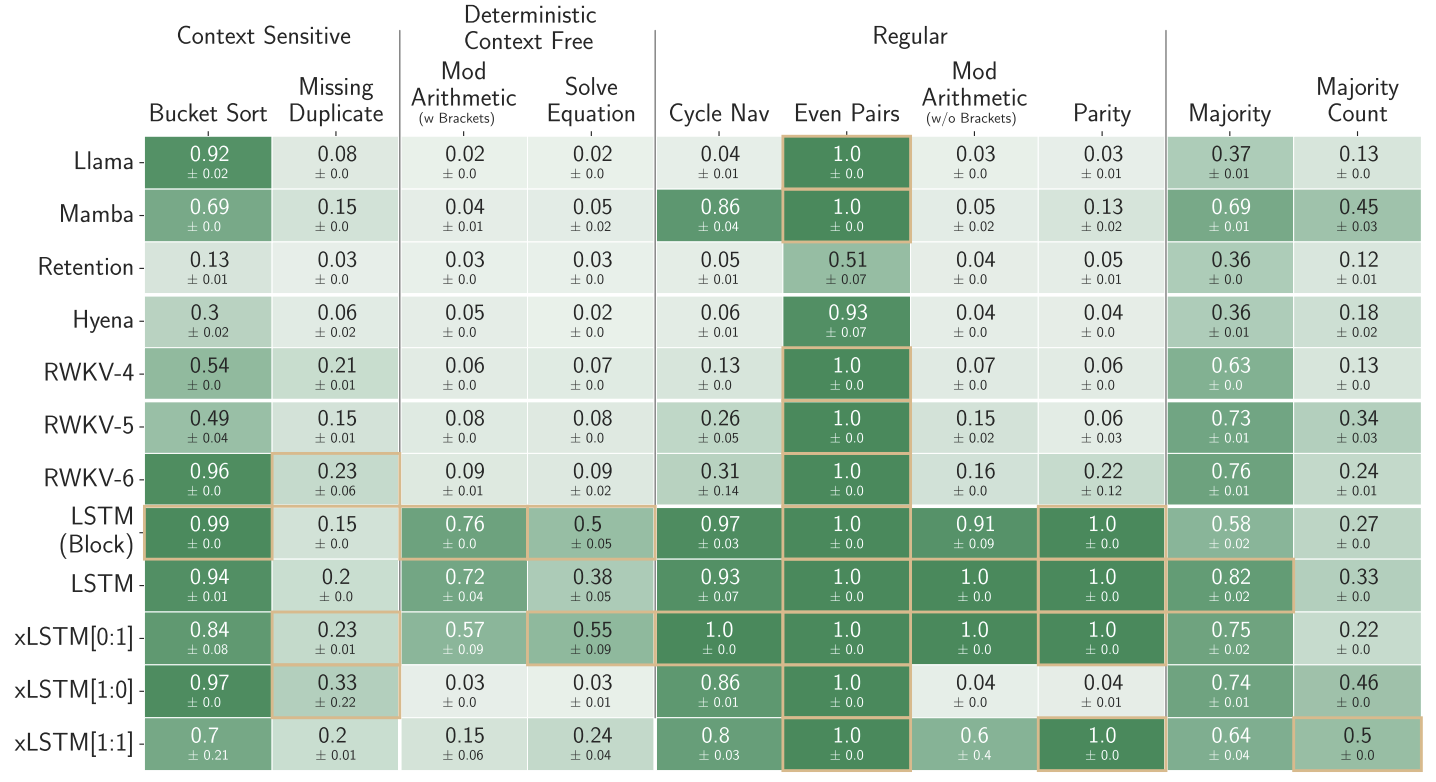
LSTM and xLSTM models far outperform Transformers and State Space Models on tasks that need long-term memory and state tracking; xLSTM, especially when combining sLSTM + mLSTM, achieves the best all-around performance, showing that recurrent memory architectures still beat attention models for logical and structured reasoning.
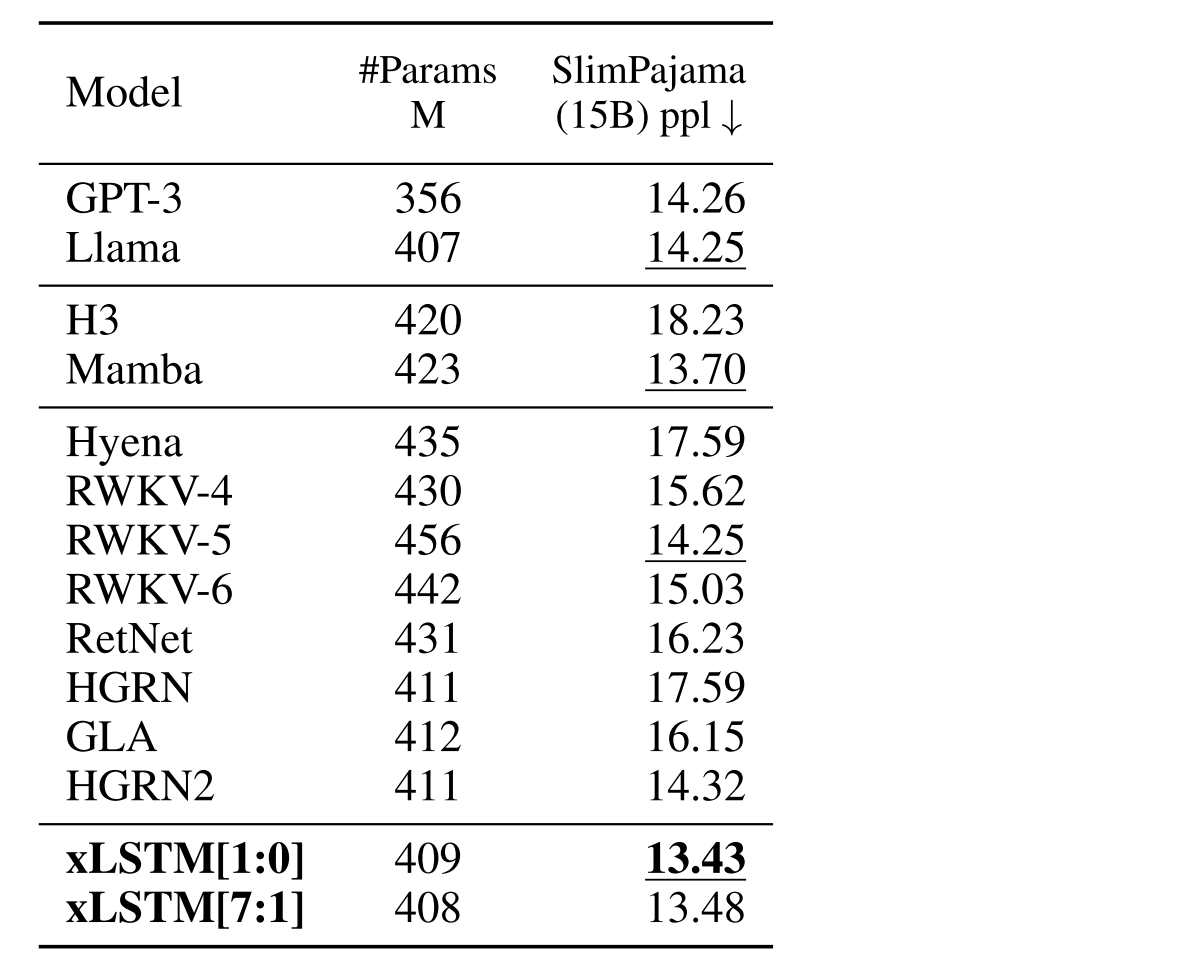
Scaling Laws
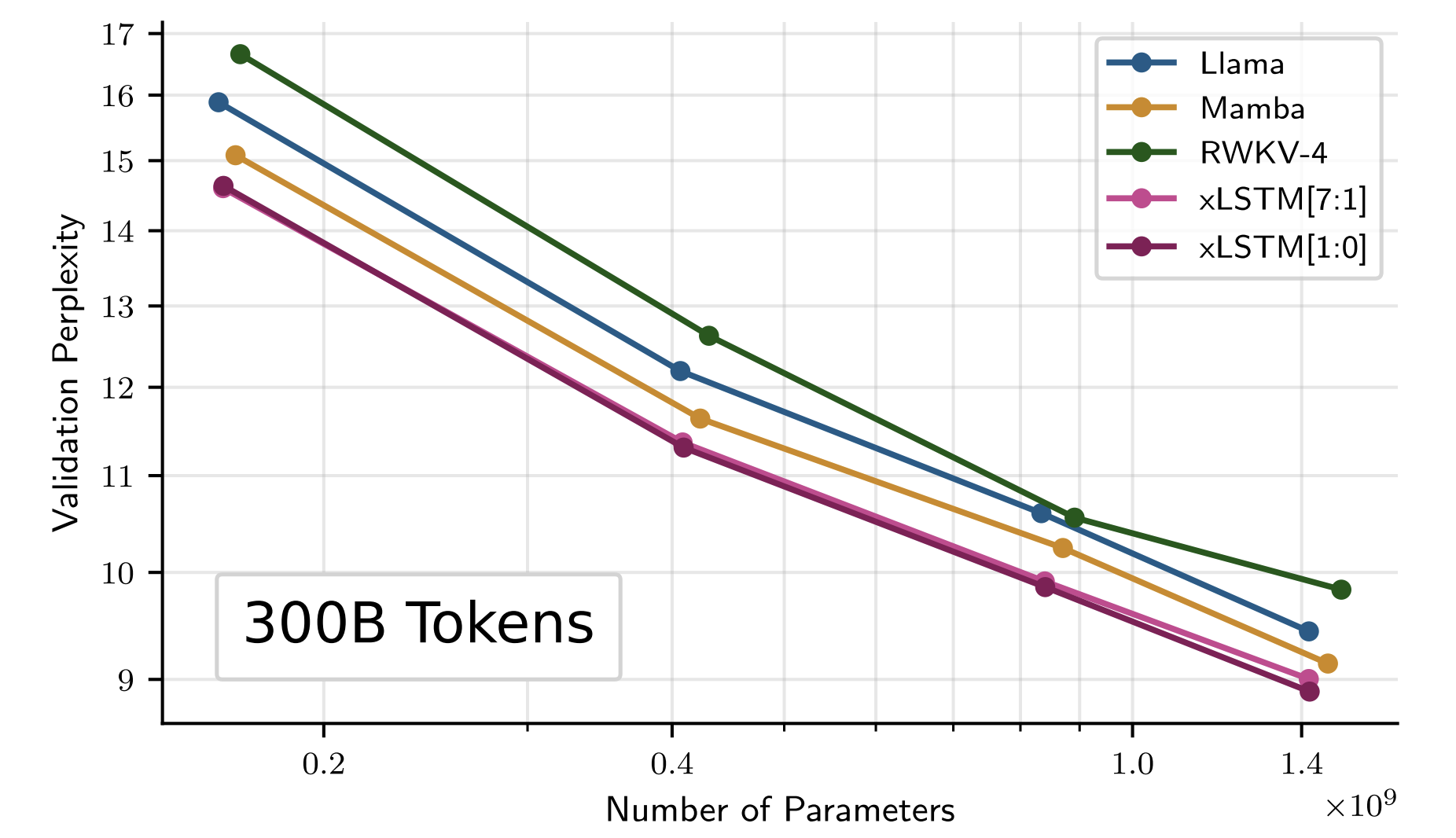
Next token prediction perplexity of xLSTM, RWKV-4, Llama, and Mamba on the SlimPajama validation set when trained on 300B tokens from SlimPajama. Model sizes are 125M, 350M, 760M, and 1.3B. The scaling laws indicate that for larger models xLSTM will perform well too.
5 Limitations
sLSTM not parallelizable:
- Its memory mixing prevents full parallel execution.
- Custom CUDA version is faster, but still ~2× slower than mLSTM.
mLSTM kernels not optimized:
- Current CUDA implementation is ~4× slower than FlashAttention.
- Could be improved with better GPU kernels.
High computation cost:
mLSTM processes (d \times d) matrices, which increases compute load,
though it can still be parallelized using standard matrix ops.
Gate initialization sensitivity:
- Forget-gate parameters must be tuned carefully for stability.
Memory limits at long contexts:
Large matrix memory may overload at very long sequence lengths,
but works fine up to ~16k tokens.
Not fully optimized yet:
- Architecture and hyperparameters weren’t exhaustively tuned due to cost.
- More optimization could further boost performance.