Introduction
Image synthesis has advanced rapidly, with diffusion models now leading in generating complex, high-resolution images. Unlike GANs, which struggle with stability and mode collapse, and autoregressive transformers, which require billions of parameters, diffusion models achieve strong results in class-conditional generation, super-resolution, and inpainting using fewer parameters and more stable training.
Despite their success, diffusion models are still computationally expensive. Because they model every pixel, including imperceptible details, both training and inference require enormous GPU time and memory. This makes them less accessible and environmentally costly.
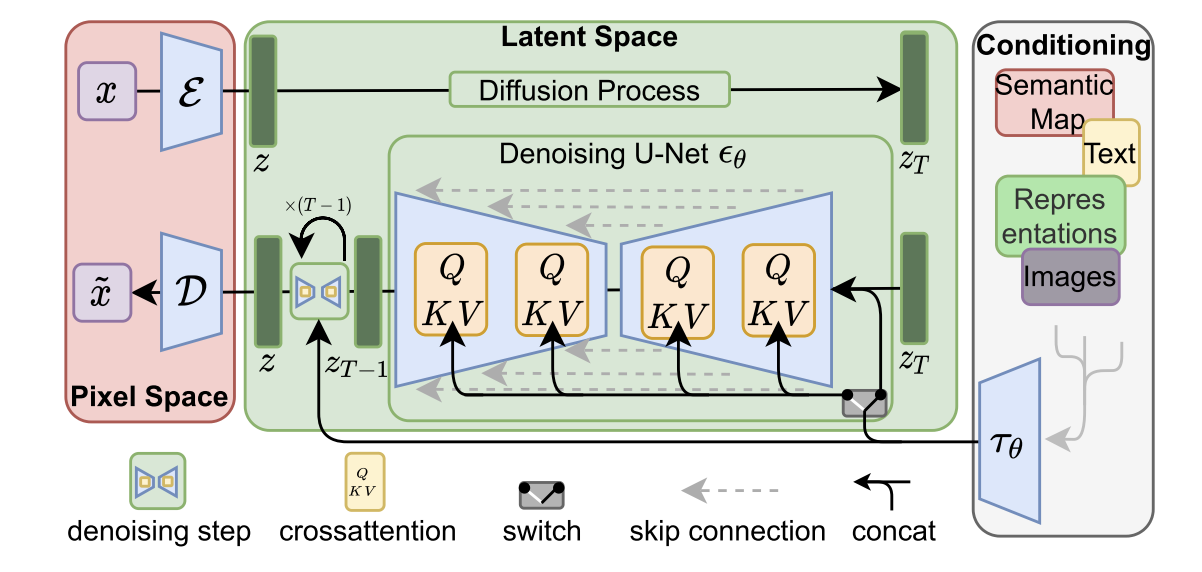
To solve this, the authors propose training diffusion models in a latent space instead of pixel space. The idea is to first use an autoencoder to compress images into a smaller, perceptually equivalent representation, and then train the diffusion model on this compact latent data. This reduces computation while keeping visual quality.
The resulting method, called Latent Diffusion Model (LDM), combines an autoencoder and a diffusion U-Net, and can include transformer-based conditioning for tasks like text-to-image generation. This design makes high-resolution synthesis more efficient and scalable.
In summary, LDMs (1) scale better to large data, (2) significantly reduce training and inference cost, (3) produce faithful, detailed reconstructions, and (4) support versatile conditioning for multi-modal tasks such as text- or layout-based image generation.
Method
The authors propose separating compression and generation into two stages. Instead of training directly in pixel space, they use an autoencoder to learn a latent space that keeps perceptual quality but greatly lowers computational complexity. The U-Net architecture further helps capture spatial structure, so there is no need for strong compression that harms image quality. In addition, the learned latent space can serve as a general-purpose representation for training other generative models or for tasks such as CLIP-guided image synthesis.
Perceptual Image Compression
The perceptual image compression model is an autoencoder trained with both a perceptual loss and a local patch-based adversarial loss to produce realistic, non-blurry reconstructions. The encoder compresses an image $x$ into a latent representation $z = ε(x)$, and the decoder reconstructs it as $\tilde{x} = D(z)$. The image is downsampled by a factor $f$.
To keep the latent space stable, two types of regularization are used: a KL penalty (as in VAEs) or vector quantization (as in VQGANs). Unlike earlier methods that flattened the latent space into one dimension, this model keeps the 2D spatial structure of the latent representation, allowing for milder compression and higher reconstruction quality while preserving fine image details.
Latent Diffusion Models
Latent Diffusion Models (LDMs) are based on diffusion models, which learn to generate data by gradually denoising random noise through a reverse Markov process. In this framework, each step predicts a cleaner version of a noisy input, trained with a simple mean-squared error objective. By applying diffusion in the latent space learned from the perceptual autoencoder, the model focuses on meaningful, semantic image features instead of pixel-level noise. Unlike previous transformer-based methods that used discrete tokens, LDMs use a U-Net built from 2D convolutions to better capture spatial image structure. During generation, latent samples are denoised step by step and then decoded into final images with a single pass through the decoder.
Conditioning Mechanisms
Conditioning mechanisms allow diffusion models to generate images based on extra input information $y$, such as text, semantic maps, or other images. To achieve this, the model learns a conditional distribution $p(z|y)$ by adding the condition $y$ to the denoising network. The authors enhance the U-Net backbone of the LDM with a cross-attention mechanism, which lets the network focus on relevant parts of $y$ while generating the image. A separate encoder $τ_θ$ converts the condition into an embedding that interacts with the U-Net through attention layers. This setup allows flexible conditioning from different modalities, meaning the same diffusion model can handle tasks like text-to-image, layout-to-image, or other image-to-image synthesis efficiently.
$$ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d}}\right) \cdot V $$
$$ Q = W_Q^{(i)} \cdot \varphi_i(z_t), \quad K = W_K^{(i)} \cdot \tau_\theta(y), \quad V = W_V^{(i)} \cdot \tau_\theta(y) $$
- $K$ and $V$ come from the conditioning input (e.g., text embeddings).
- $Q$ comes from the U-Net feature map at the current diffusion step.
Use in super-resolution
Latent Diffusion Models (LDMs) can perform super-resolution efficiently by conditioning on low-resolution images. The method simply concatenates the LR input with the U-Net input, allowing the model to learn how to reconstruct high-frequency details.
Using a pretrained autoencoder with downsampling factor (f=4), the model (LDM-SR) is trained on ImageNet with bicubic 4× downsampling, following SR3’s setup. A user study confirms that LDM-SR produces more visually pleasing results. To further enhance detail, a perceptual loss is added as a guiding mechanism. Finally, since bicubic degradation limits generalization, a more robust version called LDM-BSR is trained using diverse degradations to handle real-world low-quality inputs.
Conclusion
Latent diffusion models, a simple and efficient way to significantly improve both the training and sampling efficiency of denoising diffusion models without degrading their quality. Based on this and cross-attention conditioning mechanism, the experiments could demonstrate favorable results compared to SOTA methods across a wide range of conditional image synthesis tasks without task-specific architectures.