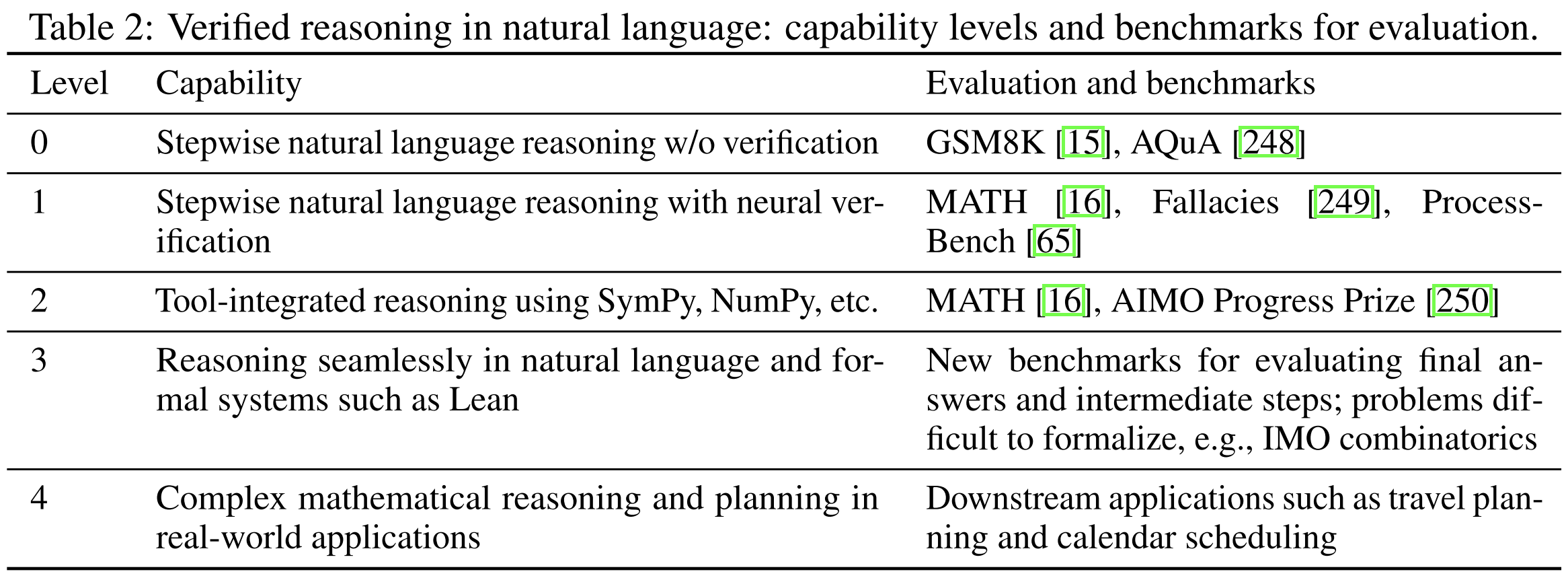
1. Introduction
1.1. Informal math LLMs have improved, but face clear limits
Most current AI4Math models use NLP-style “informal reasoning” (datasets, CoT, self-consistency).
They perform well on benchmarks like GSM8K and MATH, but this approach struggles to scale to advanced or research-level mathematics due to:
- scarcity of high-quality data
- difficulty evaluating long reasoning chains
- hallucinated or invalid reasoning
1.2. Scaling training alone is not enough
Simply making models bigger and training on more data cannot solve these limitations.
Recently, systems like OpenAI o1 try to scale inference-time reasoning (search + verification), but their effectiveness on advanced math remains uncertain.
1.3. Formal mathematical reasoning is a crucial complementary path
Formal methods use proof assistants (Lean, Coq, Isabelle) that:
- enforce strict, verifiable logic
- provide reliable feedback
- reduce hallucination
- support synthetic data generation
1.4. Recent successes show the promise of formal methods
Neuro-symbolic systems like AlphaProof and AlphaGeometry achieve breakthrough results by combining:
- symbolic formal systems (proof assiatant)→ PA
- neural reasoning models
These demonstrate that formal reasoning can scale to high-level mathematics.
1.5. The field is at an inflection point
AI-based formal mathematical reasoning is rapidly growing and has major potential for:
- advancing pure mathematics
- improving software/hardware verification
- building reliable reasoning systems
The paper argues that formal reasoning should complement informal LLM approaches to push AI4Math forward.
2. Method
2.1. Informal Reasoning LLM
NuminaMath: a math LLM for informal reasoning:
- Math pretraining
- Finetuning on step-by-step solutions
- Tool-integrated reasoning
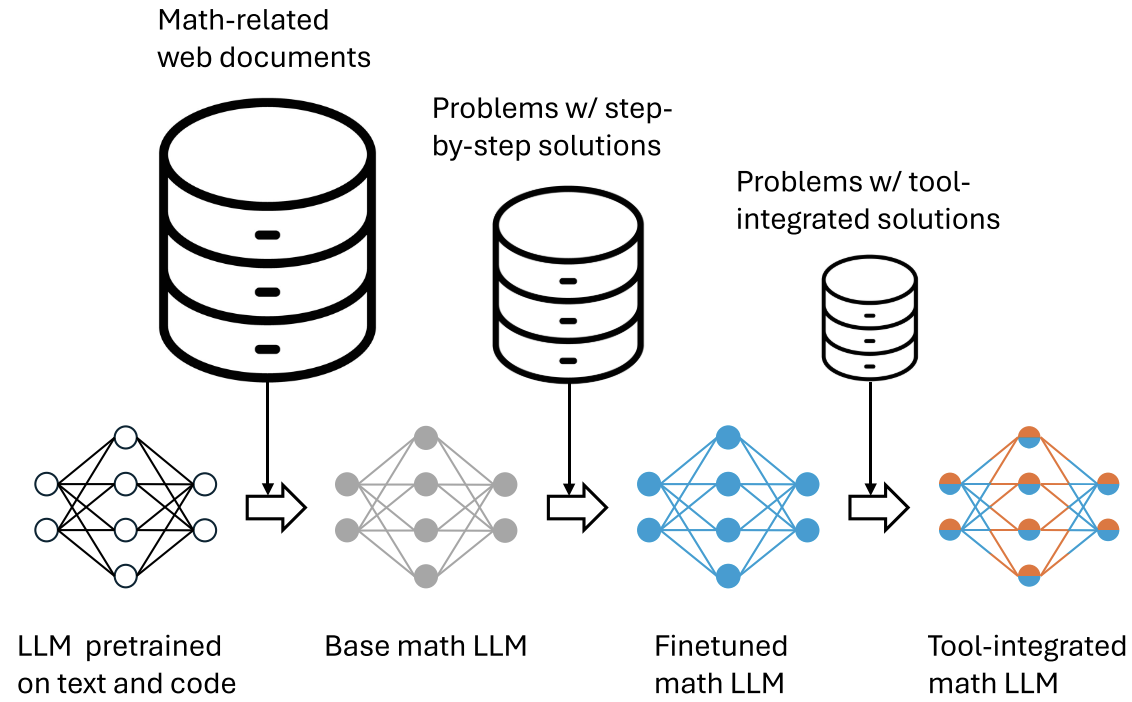
2.2. Formal Mathematical Reasoning
2.2.1. Formal Proof Assistant
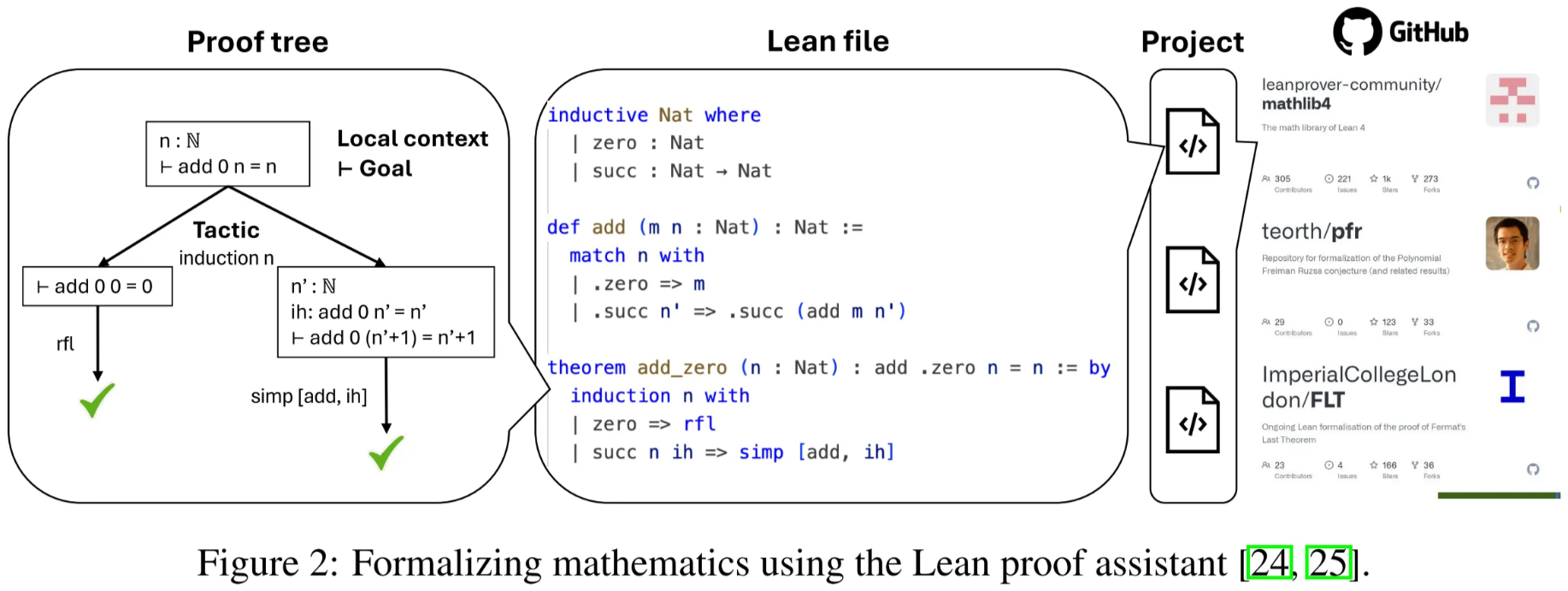
Think of Lean like a strict programming language for math:
- Proof Tree = how a single theorem is proved internally by Lean
- nodes are goals, edges are tactics
- Lean File = the code written by humans to prove the theorem
- Project = a whole project full of code
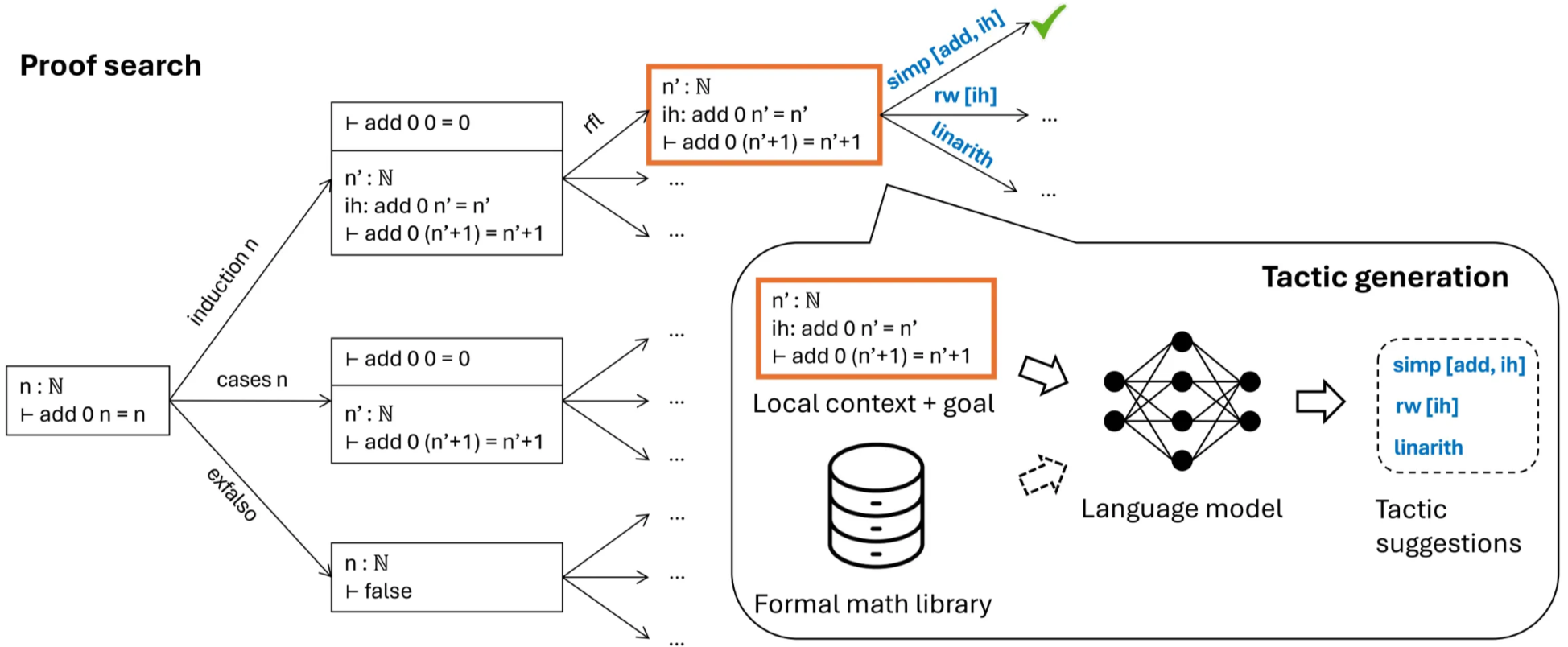
2.2.2. Neuro-symbolic Theorem Prover
3. Open Challenges and Future Directions
3.1. Data

3.2. Algorithms







3.3. Tools for Assisting Human Mathematicians

4. Milestones and Success Measures