1. Introduction
ATLAS addresses a fundamental limitation of modern recurrent memory models (e.g., Titans): they update memory token by token, using only the current key–value pair, which limits:
- Memory capacity – only O(d) independent pairs can be stored.
- Memory quality – memory captures individual tokens rather than the structure of a context span.
- Memory optimization – update rules (e.g., gradient descent + momentum) are simple and often sub-optimal.
- Scalability – sequential updates reduce parallelization.
To overcome these issues, ATLAS proposes a more expressive and scalable framework in which:
- Memory is a deep MLP updated during inference (like Titans),
- but the update rule optimizes memory w.r.t. a whole context window,
- using richer feature mappings and a stronger internal optimizer.
This allows the model to memorize context, not just individual tokens, while retaining RNN-style linear complexity.
2. Method
The ATLAS framework has three core components:
2.1. High-capacity memory via polynomial feature mapping
Instead of using raw keys $k$, ATLAS applies a feature map $\phi(k)$:
- Polynomial kernels increase effective dimensionality from $d → O(d^p)$.
- Exponential kernels approximate the exponential $q^T k$ of Transformers.
This dramatically increases memory capacity without increasing the number of memory parameters.
2.2. Context-aware memory update (Omega Rule)
Unlike Titans (which update with only $(k_t, v_t)$),
ATLAS updates memory using a sliding window of the last c tokens:
$$ M_t = \arg\min_M \sum_{i=t-c+1}^{t} Y_i^{(t)} | M(\phi(k_i)) - v_i |^2 $$
Features:
- Multi-token optimization: memory learns from a context span, not a single token.
- Learned gates $Y_i^t$: controls how much each token contributes.
- Generalizes classical rules:
- $c=1$ → Delta rule / Titans
- $c=\infty$ → global optimization like attention
2.3. Stronger internal optimizer (Muon)
ATLAS replaces Titans’ first-order memory update (gradient descent + momentum):
$$ M_t = \alpha_t M_{t-1} + S_t,\qquad $$
$$ S_t = \gamma_t S_{t-1} - \eta_t \nabla \ell(M_{t-1}; k_t, v_t) $$
with a second-order, quasi-Newton style update using the Muon optimizer.
Muon approximates the Newton update:
$$ M_t = M_{t-1} - H_t^{-1} \nabla \ell_t, $$
and replaces $H_t^{-1}$ with a cheap matrix-free approximation using the Newton–Schulz iteration:
$$ H_t^{-1} \approx \text{NS}(G_t), $$
where $G_t$ is an approximate curvature / preconditioner matrix.
Thus, the ATLAS memory update using Muon becomes:
$$ M_t = \alpha_t M_{t-1} - \eta_t \text{NS}(G_t) , \left( \sum_{i=t-c+1}^{t} Y_i^{(t)} \nabla \ell(M_{t-1}; k_i, v_i) \right), $$
where:
- $\alpha_t$ = learned forget gate
- $\eta_t$ = learned step size
- $Y_i^{(t)}$ = per-token contribution gate
- $\text{NS}(G_t)$ = Muon second-order curvature approximation
Training & parallelization
To make Omega Rule scale to long sequences, ATLAS:
- splits the sequence into parallel chunks,
- applies recurrent updates within a chunk,
- and applies parallelizable gradient accumulation across chunks.
Thus ATLAS preserves the GPU/TPU-friendly nature of Titans while significantly improving memory quality.
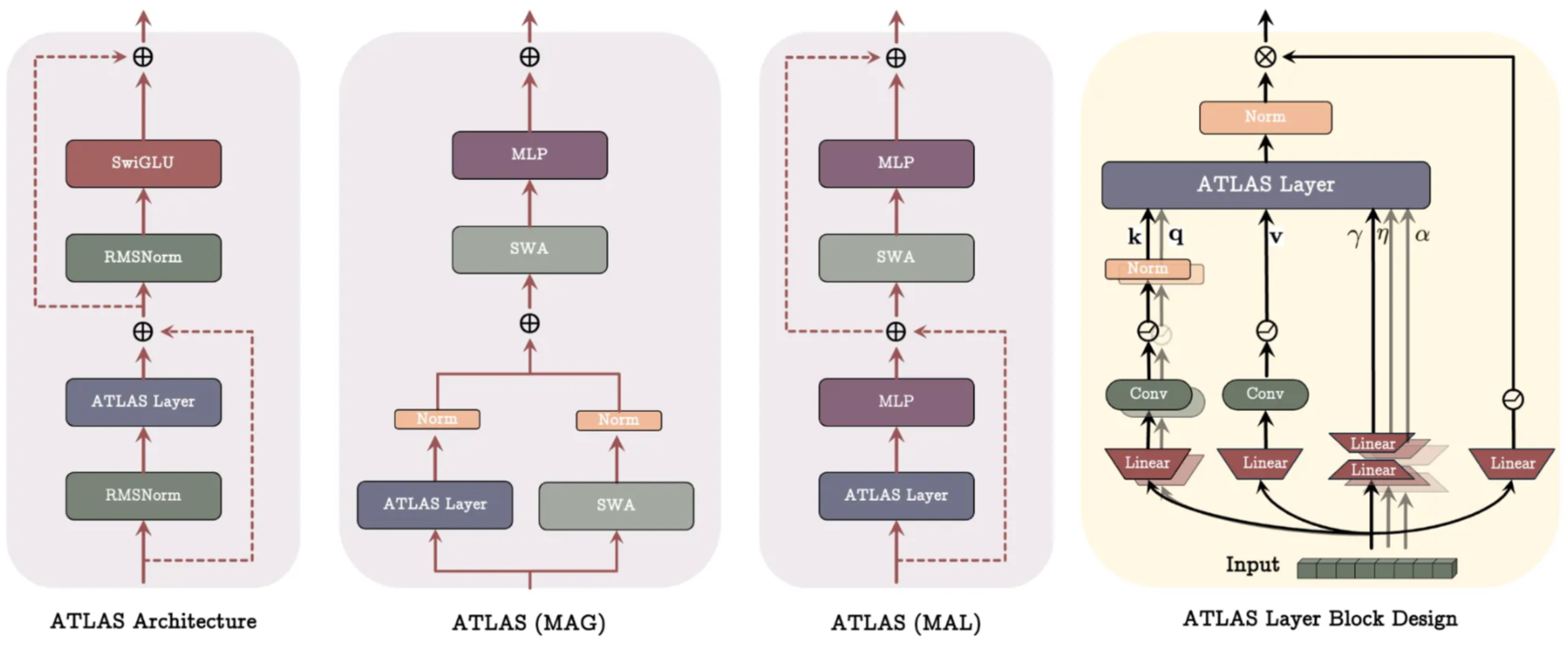
3. Novelty
Attention replacement with linear complexity
ATLAS Layer substitutes the Transformer attention block with a read–write memory module that enables long-context reasoning at O(n) cost.
Context-based memory updates
ATLAS replaces token-level updates (Titans) with the Omega Rule, optimizing memory over a window of past tokens rather than only the current one.
Deep neural memory with high capacity
The memory is a deep MLP whose parameters are updated at inference.
Polynomial/exponential feature maps expand keys/queries and give super-linear memory capacity.
Second-order test-time learning
Memory updates use the Muon optimizer, a quasi-Newton method, providing more stable and expressive learning than Titan’s first-order gradient descent.