1. Method
1.1. Replace self-attention with a 2D Fourier Transform
FNet removes the entire self-attention sublayer from Transformer encoders. Instead, each layer performs a 2D Discrete Fourier Transform (DFT) on the input:
$$ y = \Re\left(F_{\text{seq}}(F_h(x))\right) $$
- $F_{\text{seq}}$: 1D DFT along the sequence length
- $F_h$: 1D DFT along the hidden dimension
- The discrete Fourier Transform (DFT) is defined by the formula:
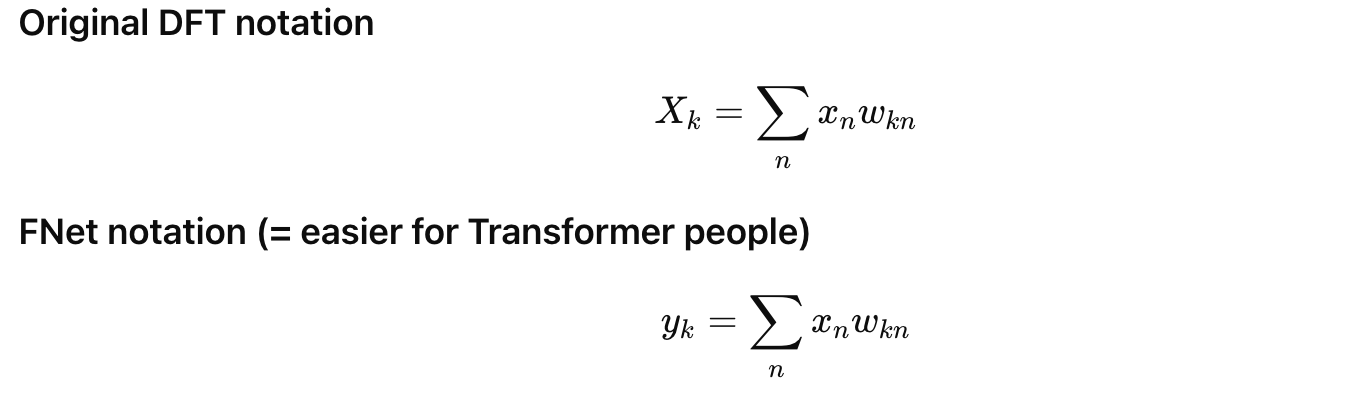
Thus, no Q/K/V, no dot-products, and no softmax are computed.
1.2. Simple Transformer-style architecture
Each encoder block contains:
- Fourier mixing sublayer (parameter-free)
- Feed-forward network (FFN)
- Residual + LayerNorm (same as BERT)
The model uses the same word/type/position embeddings as BERT, but position embeddings are technically unnecessary because the Fourier basis already encodes position.
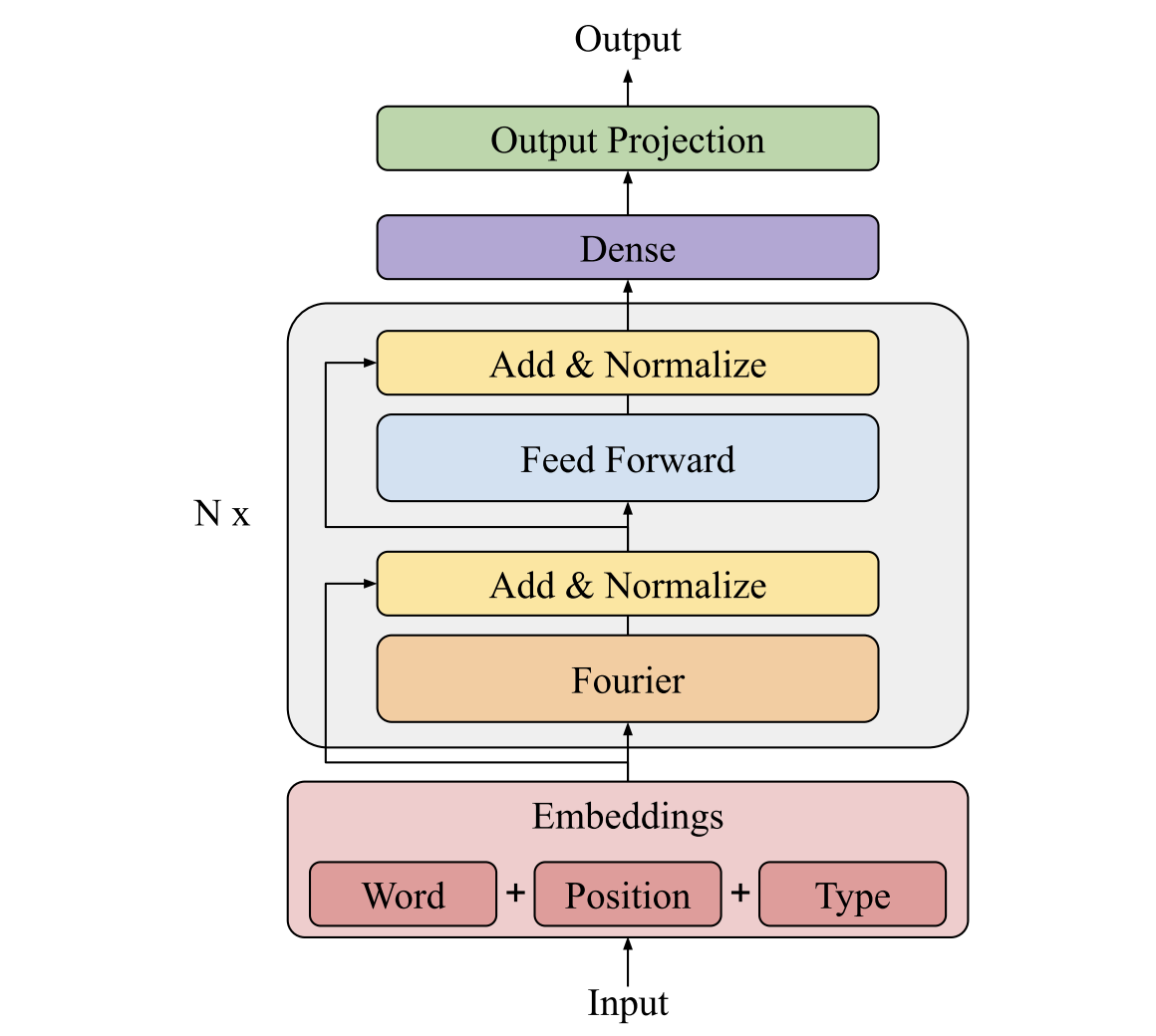
FNet architecture with N encoder blocks.
1.3. Computational efficiency
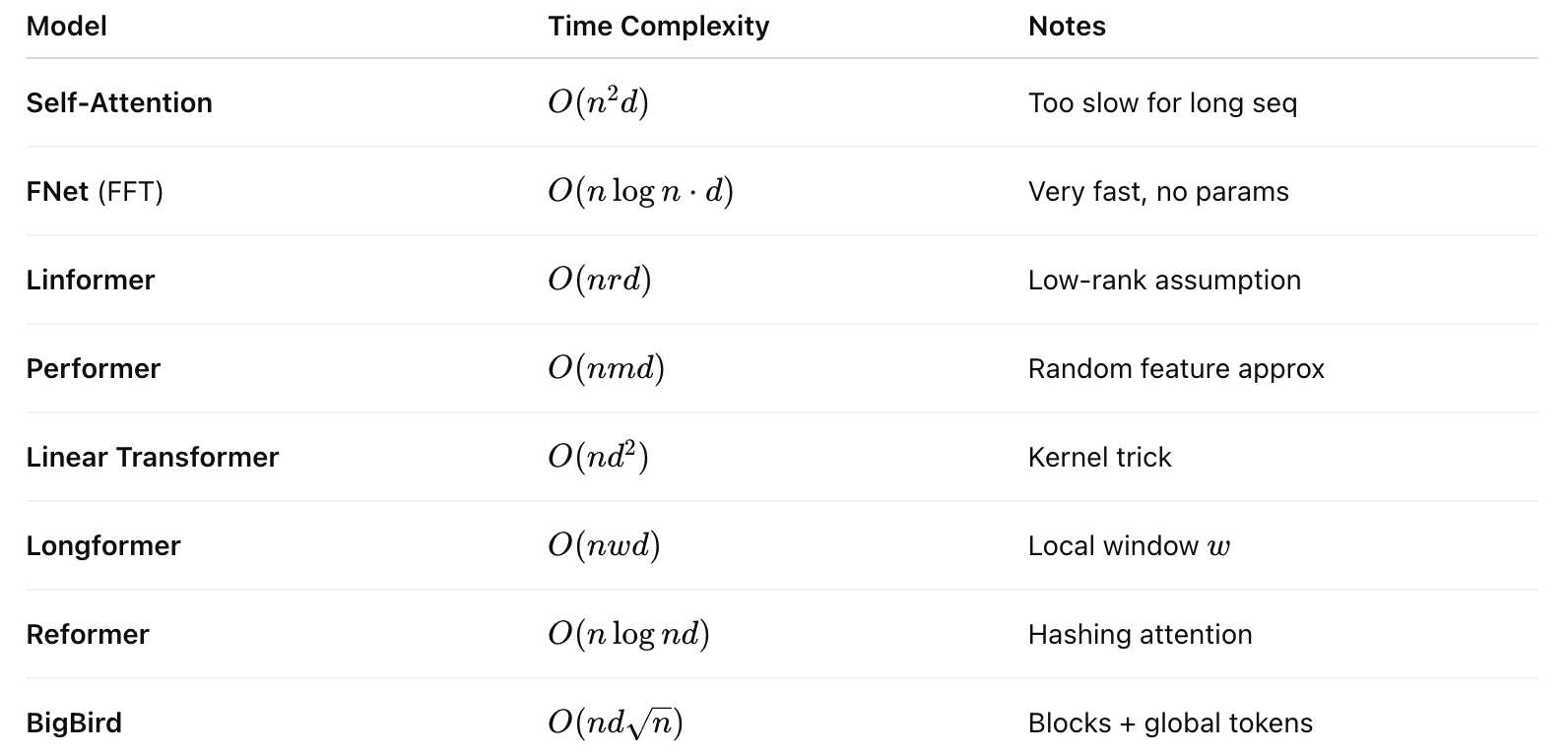
The FFT has complexity: $O(n \log n d)$ because of FFT (Fast Fourier Transform).
Compared to self-attention: $O(n^2 d)$
This yields major speedups:
- 80% faster training on GPUs,
- 70% faster on TPUs,
- Much faster for long sequences (LRA benchmark).
2. Novelty
2.1. First model to fully replace attention with Fourier mixing
Previous works used Fourier features to approximate attention (e.g., Performer).
FNet is the first to:
Remove self-attention entirely and use a fixed, unparameterized Fourier Transform as the token-mixing mechanism.
The mixing weights come purely from:
$$ e^{-2\pi i nk / N} $$
and not from learned Q·K projections.
2.2. Demonstrates that structured linear mixing can rival attention
A surprising empirical finding:
- FNet reaches 92–97% of BERT’s accuracy on GLUE
- Despite having zero learned parameters in its mixing layer
This suggests:
Attention is not always the main source of performance;
high-quality token mixing + FFN may be sufficient for many NLP tasks.
2.3. Superior long-sequence scalability
On the Long-Range Arena (LRA) benchmark:
- FNet matches the accuracy of the strongest models
- But is faster and more memory-efficient than Performer, Linformer, and other efficient Transformers
This shows a new path:
Instead of approximating attention, one can replace it with a simpler mathematical transform.
2.4. Extremely good small-model efficiency
For smaller models, FNet and Linear mixing form the Pareto frontier for speed–accuracy (Fig. 2).
Because Fourier mixing is parameter-free:
- Smaller memory footprint
- High stability during training
- Better deployment potential on edge devices
3. Why is DFT a mixing operation like attention?
Because:
$$ X_k = \sum_{n=0}^{N-1} w_{kn} \cdot x_n $$
Where:
$$ w_{kn} = \cos(2\pi nk / N) $$
This is EXACTLY what attention does:
$$ y_i = \sum_j W_{ij} \cdot x_j $$
The only difference:
| Mechanism | Weights ( W ) |
|---|---|
| Attention | Learned from Q·K |
| Fourier / DFT | Fixed sine/cosine patterns |
Both compute:
Output token = weighted sum of all input tokens
Therefore both are global mixing layers.
4. Summary Table of Time Complexities