⁉ Why Is Hyperparameter Tuning So Difficult?
Bengio’s Classic Paper Tells You: Stop Using Grid Search!
In machine learning, there’s a saying:
“Training the model is easy. Tuning hyperparameters is hell.”
Learning rate, number of layers, regularization strength, hidden units…
Everything seems important, but tuning them feels like opening blind boxes.
Today we look at a classic paper from Yoshua Bengio’s team:
“Random Search for Hyper-Parameter Optimization.”
Its key message is surprisingly simple:
Random Search is far more efficient than Grid Search.
It’s cheaper, faster, and works especially well in high-dimensional spaces.
Let’s walk through the core ideas of this paper in a beginner-friendly way.
❓1. Why Is Traditional Grid Search Inefficient?
The goal of hyperparameter optimization is simple:
Find a set of hyperparameters λ that gives the best generalization performance.
The usual routine:
- Try many λ combinations
- Train models
- Evaluate on validation data
- Pick the best
But here’s the problem:
Grid Search does this:
- Pick several values for each hyperparameter
- Try every combination
As the number of hyperparameters grows, the number of combinations grows exponentially.
📌 The paper notes:
Grid Search suffers badly from the curse of dimensionality.
Even worse:
As shown later in the paper:
- For a given dataset, only 1–3 hyperparameters significantly affect performance
- Many others barely change anything
- But Grid Search still allocates equal effort across all dimensions
In simple words:
Grid Search wastes massive compute exploring unimportant directions.
🤓 2. Key Conclusion of the Paper: Random Search Is Better
The authors make a bold claim:
Random Search is more efficient and often finds better models.
And the reasoning is intuitive:
2.1. Random Search focuses more effectively on “important dimensions”
If only 1–2 hyperparameters matter:
- Grid Search: spreads effort unnecessarily across all dimensions
- Random Search: each sample covers all dimensions, increasing the chance of hitting useful values
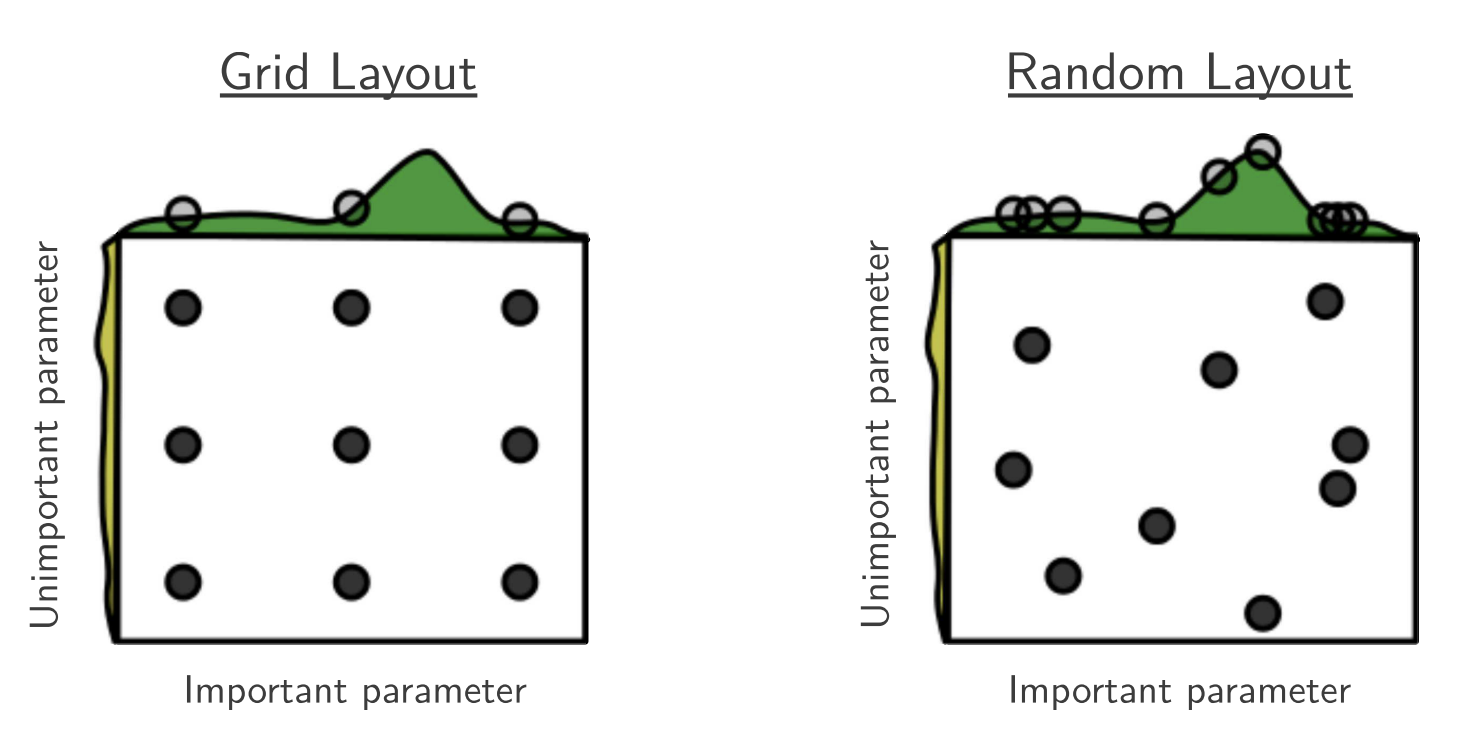
The following figure illustrates:
- In a 2D function where only x matters,
- Grid Search tests only a few distinct x-values,
- Random Search can test many more unique x-values with the same budget.
2.2. Random samples are independent (i.i.d.)
This gives several engineering advantages:
- You can stop early
- You can add more trials anytime
- Trials naturally run in parallel, asynchronously
- Failed runs don’t affect anything
It’s simple, robust, and flexible.
🔬 3. Experiments Show: Random Search Finds Better Models Faster
The paper reproduces classic deep learning experiments on datasets like:
- MNIST variants
- rectangles
- convex
- plus experiments with DBNs involving 32 hyperparameters
🔥 The results are striking:
✔ With the same compute budget:
Random Search needs only:
- 8 trials to match Grid Search’s performance at 100 trials
- 32 trials to outperform Grid Search
✔ In high-dimensional DBN tuning:
Random Search performs:
- Better on 1 dataset
- Comparable on 4 datasets
- Slightly worse on 3 datasets
In short:
Random Search is cheaper, faster, and still high-quality.
🧠 4. A Hidden Highlight:
How to Fairly Evaluate the “Best Model” from Hyperparameter Tuning?
Because the validation set is finite:
The hyperparameter with the best validation score might not truly be the best.
It may just have been “lucky” on this particular validation split.
The paper proposes:
✔ Don’t report the test performance of only the single best λ.
Instead:
✔ Report a weighted average of test performances across all λ candidates.
The weight comes from:
The probability that each λ would be the winner
(considering validation noise and variance)
This gives a more robust, unbiased, and fair estimate of generalization.
📈 5. Why You Probably Should Stop Using Grid Search
The conclusion states clearly:
- Grid Search wastes computation
- Random Search is more efficient in high-dimensional spaces
- Random trials are easy to parallelize
- Random Search should be the standard baseline for evaluating new tuning algorithms
The implicit message:
Unless you have only 1–2 hyperparameters, avoid Grid Search.
⭐ 6. Practical Takeaways:
Start Using Random Search for Hyperparameter Tuning!
One-sentence summary of the paper:
Grid Search is inefficient; Random Search is faster and finds better results.
Why Random Search works better:
- Real models have low effective dimensionality.
- Grid Search wastes effort in irrelevant dimensions.
- Random Search offers wider, more meaningful exploration.
- It’s parallel-friendly and simple to implement.
A practical tip:
If you have more than 2 hyperparameters, Grid Search is almost always a bad idea.
📌 7. Practical Advice for ML Engineers & Students
✔ Prefer Random Search over Grid Search
(even for neural networks and classical ML)
✔ If budget permits
Upgrade to Bayesian Optimization
✔ When tuning many hyperparameters (>20)
Use:
Random Search + Early Stopping
It often delivers surprisingly strong results.
🏁 Final Golden Sentence
Random Search isn’t “trying things randomly”; it’s statistically one of the smartest ways to tune models.